Wärmeströmung /-konvektion

Wärmeübergangskoeffizient durch Konvektion (außen)

Es ist ein Proportionalitätsfaktor α (neues Symbol für α nach Euronorm : h). Er stellt den Wärmestrom dar, der auf 1 m² Wandfläche je Kelvin Temperaturgefälle übergeht. h ist nicht wie λ ein Stoffwert. Eine ausführliche Beschreibung mit Berechnungsbeispiel ist unter Wärmeübergangskoeffizient (innen) dargestellt.

Vereinfacht wird im Bauwesen mit dem Wärmeübergangswiderstand 1/h_e = 0,04 m²K/W gerechnet, was einem Wärmeübergangskoeffizient h_e = 25 W/m²K entspricht.

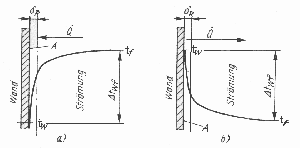
Bild Temperaturverlauf beim Wärmeübergang
a) Wärmeübergang vom Medium an die Wand
b) Wärmeübergang von der Wand an das Medium

Bei optimaler Gebäudelage kann in der Praxis durchaus eine wesentlich geringere Luftbewegung vorliegen, sodass der Wärmeübergangskoeffizient h_e nur 10 W/m²K und 1/h_e = 0,1 m²K/W betragen sollte.

Aber auch im Gebäude inneren kann durch eine Strahlenheizung und günstige Raumgeometrie eine niedrige Luftbewegung vorliegen, sodass statt des rechnerischen Wärmeübergangswiderstandes 1/h_i = 0,13 m²K/W, z. B. h_i = 0,26 m²K/W ergibt. Allein durch diesen niedrigeren Wärmeübergang an den Oberflächen treten Verbesserungen auf.

Der Wärmedurchgangskoeffizient in [W/m²K] berechnet sich nach:

1 1 1 u = --- = ------------ = ----------------------- R_k R_i + R + R_e 1 1 1 --- + --- + --- h_i Λ h_e

U = Wärmedurchgangskoeffizient in W/m²K
R_k = gesamter Wärmedurchgangswiderstand in m²K/W
R_i = Wärmeübergangswiderstand auf der Innenseite des Bauteils in m²K/W
R_e = Wärmeübergangswiderstand auf der Außenseite des Bauteils in m²K/W
R = Wärmedurchlasswiderstand in m²K/W
h_i = Wärmeübergangskoeffizient Innen in W/m²K
h_e = Wärmeübergangskoeffizient Außen in W/m²K
Λ = Wärmedurchlasskoeffizient in W/m²K

Zum Beispiel bei einer massiven Wand 40 cm Ziegel (1800 kg/m³), Kalkputz innen 1,5 cm und Kalkzementputz außen 2 cm und λ= 0,81 W/mK, 1/h_e = 0,04 m²K/W und 1/h_i = 0,13 m²K/W ergibt ein Wärmedurchgangskoeffizient u = 1,51 W/m²K.

Treten in der Praxis geringere Luftströmungen auf ( 1/h_e = 0,1 m²K/W und 1/h_i = 0,26 m²K/W), so ergibt sich eine Verbesserung von 30 % ( u = 1,17 W/m²K).

Liegt dagegen eine höhere Luftbewegung an einer Außenwand (meistens eine Giebelwand) durch Staudruck vor, so verschlechtert sich der rechnerische Wärmedurchgangskoeffizient! Aber es ist anzunehmen, dass sich diese Situation auch auf die Innenseite der Außenwand auswirkt und sich die Luftströmung auch an der inneren Wandoberfläche erhöht. Der Wärmeübergangswiderstand 1/h_i = 0,13 m²K/W verringert sich. Ist dieser nur noch halb so groß, und es wird für 1/h_e = 0,01 m²K/W und 1/h_i = 0,065 m²K/W angenommen, so ergibt sich für den Wärmedurchgangskoeffizienten etwa 1,76 W/m²K. Es erfolgt eine Verschlechterung von circa 17%.

Bei gleichem Wandaufbau aber unterschiedlich hoher Luftgeschwindigkeit liegt bei diesen Berechnungsbeispielen ein U-Wert zwischen 1,17 bis 1,76 W/m²K vor, eine Differenz von circa 50%. In der Praxis können diese Werte noch größer sein.

Besteht die Außenwand aus 40 cm Leichtziegel + Putz mit λ= 0,14 W/mK, so liegt der Wärmedurchgangskoeffizient U = 0,33 W/m²K. Bei diesem niedrigen U-Wert hat die rechnerische Wertung der Wärmeströmung (Konvektion) nur noch einen kleinen Einfluss. Bei kleineren Luftströmungen ( 1/h_e = 0,1 m²K/W und 1/h_i = 0,26 m²K/W) ergibt sich ein U-Wert von 0,31 W/m²K).
Allerdings nimmt das Verhältnis des erforderlichen Lüftungswärmeverlustes bei einer hochgedämmten Außenwand zu, siehe hierzu Verhältnis hohen Lüftungswärmeverlust.

Zum Wärmeübergangswiderstand