Im Bauwesen spielt die Bestimmung der absoluten Feuchte für den gekoppelten Feuchte- und Wärmetransport durch eine mineralische Wand sowie für die Tauwasserbildung an kühlen Oberflächen oder an einer Sperrschicht eine wichtige Rolle.
In das kleine Berechnungsprogramm können Sie die einzelnen Werte, wie gemessene Temperatur der Luft und die relative Luftfeuchte eingeben und erhalten somit die absolute Feuchte. Geben Sie eine niedrigere Temperatur ein, zum Beispiel von der Außenluft im Winter, auch wenn diese eine höhere relative Luftfeuchte hat, so verringert sich der angezeigte Wert der absoluten Feuchte. In diesem Fall macht eine Lüftung zur Reduzierung der Feuchte in den Räumen einen Sinn. Wobei die relative Luftfeuchte wegen der Behaglichkeit, siehe Klimawerte, einen bestimmten Wert entsprechen sollte und nicht zu trocken ist. Wichtig ist auch zu wissen, dass bei gleicher Temperatur, die feuchtere Luft mehr Energie beinhaltet. Das wird im Artikel zum Mollier h,x-Diagramm erläutert. Die energiereichere feuchte Raumluft wird durch das Lüften durch energieärmere trockenere Außenluft ausgetauscht. Um nicht unnötig viel Heizenergie zu verbrauchen, ist eine sinnvolle Lüftung einzuhalten.
Den ungünstigsten Fall für eine Lüftung stellt die schwülwarme Außenluft im Sommer dar. In den meisten Fällen wird beim Lüften zusätzlich Feuchtigkeit in die Wohnung gelüftet.
Ebenso ist für vielen technische Prozesse die Bestimmung der absoluten Luftfeuchte von Bedeutung. Hier wird nur ein eingeschränkter Überblick zur Berechnung der absoluten Feuchte vermittelt. Für vertiefende Ausführungen sollte die entsprechende Fachliteratur studiert werden.
In der Luft ist Wasserdampf enthalten. Die Menge an Wasser, gerechnet als Masse des Wasserdampfes in kg pro kg Luft, bezeichnet man als absolute Feuchte x.
Die maximale absolute Feuchte ist derjenige Gehalt an Wasserdampf pro m3 Luft, der bei Sättigung der Luft mit Wasserdampf aufgenommen werden kann. Je wärmer die Luft, desto mehr Wasserdampf kann sie aufnehmen.
Sinkt die Temperatur der Luft, so bildet sich Nebel/Regen als Kondensat, wenn die Sättigungsfeuchte der jeweiligen Lufttemperatur erreicht wird.
RG φ * ps x = ---- -------------- oder RD p - φ * ps x * p φ = ----------------- ps ( RG/RD + x)
RG = 287,1 Nm/kgK (Gaskonstante für Luft)Der Teildruck pD des Dampfes kann nicht beliebig groß sein, sie wird durch die gegebene Gemischtemperatur bestimmt. Der Dampf kann höchstens den durch die Dampfspannungskurve gegebenen Druck ps haben.
Es gilt für ungesättigte Luft φ * ps x = 0,622 * ------------- kg/kg p - φ * ps und für gesättigte Luft ps x = 0,622 * --------- kg/kg p - ps Im Volumen enthaltene Dampfmasse φ * ps mD = --------- * V RD * T
Beispiel: Ein Zimmer mit einem Raumvolumen von 50 m3 und einer relativen Luftfeuchte φ = 0,5 bei p = 100 KPa, ps290 K = 1936,3 Pa = 1936,3 N/m2 und ϑ = 17ºC = 290 K. Gesucht ist die Masse des enthaltenen Dampfes.
φ * ps mD = --------- * V RD * T 0,5 * 1936,3 N/m2 = -------------------------- * 50 m3 461,5 Nm/kgK * 290 K = 0,362 kg Wasserdampf
Die Luft mit dem Raumvolumen von 50 m3 enthält 0,362 kg Wasserdampf.
Ein Mensch atmet circa 100 g Wasser pro Stunde aus. Während der Nachruhe sind dies zirca 800 bis 1000 g. Das oben genannte Volumen entspricht etwa einem Raum von 5 m x 4 m. Es soll geprüft werden, wie groß die relative Luftfeuchte nach 4 Stunden ist, wenn während dieser Zeit keine Lüftung erfolgt. Wasserdampfmenge 362 g + 400 g = 762 g .
mD * RD * T φ = ---------------------- ps * V 0,762 kg * 461,5 Nm/kgK * 290 K = ------------------------------------- 1936,3 N/m2 * 50 m3 = 1,05 (φ= max. 1,0 möglich.)
Bei diesem Beispiel wird deutlich, je dichter die Fenster im Schlafzimmer sind, umso schneller steigt die Luftfeuchtigkeit an. (In der Praxis wird ein Teil dieser Feuchtigkeit kurzfristig durch die Wandbaustoffe und Einrichtungsgegenstände aufgenommen, sodass φ nie 1 wird.)
Die maximale Menge an Wasserdampf, die die Luft mit 17ºC aufnehmen kann, berechnet sich nach folgender Formel (für ps290K = 1936,3 N/m2 bei p = 100 kPa siehe Tabelle 1) oder siehe auch die Dampfsättigungskurve. (Bei der Berechnung wird mit bar gerechnet, daher eine kleine Abweichung.)
φ * ps mD = ------------ RD * T 1,0 * 1936,3 N/m2 = -------------------------- 461,5 Nm/kgK * 290 K = 0,01446 kg Wasserdampf
(Statt Komma Dezimalpunkt eingeben.)
*)Dieser Wert ist gerundet
Es treten geringe Abweichungen zum oben genannten Beispiel auf, da statt Pa mit bar gerechnet wird.
| Tabelle 1: ps bei 100 kPa (Auszug aus Meyer S.364) | |
| 268 K | 401,1 Pa |
| 273 K | 610,8 Pa |
| 278 K | 871,8 Pa |
| 283 K | 1227,1 Pa |
| 288 K | 1704,0 Pa |
| 290 K | 1936,3 Pa |
| 293 K | 2337,0 Pa |
| 298 K | 3167 Pa |
| 303 K | 4241 Pa |
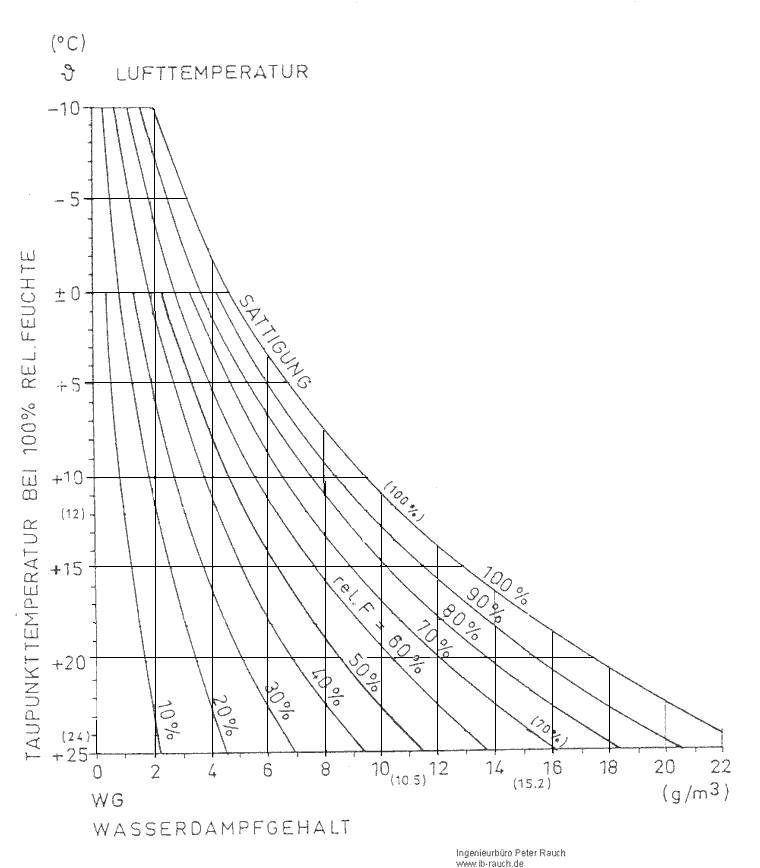
Statt der Berechnung kann man die jeweiligen Werte der nachfolgenden Grafik entnehmen (auf Bild klicken).
Erste Tipps zur Schadensbeseitigung bei Gebäuden durch Hochwasser,
Feuchteprobleme bei Gebäuden nach Wassereinwirkung und Bauteilbetrachtung (Skizzen),
Warum sind Wasserschäden im Haus schnell zu beseitigen?
Hochwasserschäden an Gebäude - Sanierungsmaßnahmen und
Hochwasserschäden an Lehmhäuser.
Quelle:
Meyer, Günter; Schiffner, Erich; Technische Thermodynamik, 2. Aufl. Fachbuchverlag Leipzig 1983, S. 189, 191
© Altbausanierung | Bauideen | Download | Impressum | Datenschutzerklärung | 3/2006 
