2. Die
Einflussnahme der Wärmekonvektion auf die
Oberflächentemperatur
3. Warum ist eine Erhöhung der Oberflächentemperatur in der Raumecke erforderlich?
4. Der Einfluss der Temperaturstrahlung im Gebäude
Von besonderer Bedeutung ist die Innenseite einer Gebäudeecke. Viele Schimmelpilzschäden treten gerade in den unteren Bereichen der Außenwandecken auf. Dabei treten Temperaturdifferenzen von 7 bis 10 K gegenüber der Raumlufttemperatur auf. Im Extremfall können hier auch noch größere Differenzen entstehen.
Bild: Schimmelpilzbildung an einer Gebäudeaußenecke. Raumlufttemperatur 17,6°C bei einer relativen Luftfeuchte von 53%
Die Folge ist eine Tauwasserbildung an der Wandoberfläche bzw. es stellt sich unmittelbar an der Oberfläche eine hohe relative Luftfeuchte ein. Aber auch bei neuen Gebäuden mit einem Wärmedämmverbundsystem werden messtechnisch Temperaturdifferenzen ermittelt, die zu einer Schimmelpilzbildung führen. In einer Untersuchung, wo zwei verschiedene Wandkonstruktionen mit und ohne Wärmeverbundsystem mit gleichem U-Wert bewertet werden, zeigt sich, dass die Temperatur im Eckbereich der monolithischen Wand nur um circa 1K niedriger ist. [19] Damit scheint ein Wärmeverbundsystem dieses Problem an dem geometrischen Bauteilabschnitt nicht vollständig zu lösen. In diesem folgenden Abschnitt wird abweichend von der DIN (DIN EN ISO 6946, DIN 4108-3, DIN EN ISO 10211-1) eine andere Sichtweise zur Bewertung des geometrischen Bauteilabschnittes gewählt.
In zahlreichen Publikationen werden rechnerisch ermittelte Isotherme im massiven Wandquerschnitt [12, 16, 17, 18] oder mit Hilfe von Infrarotaufnahmen Temperaturunterschiede gezeigt. Was auf dem ersten Blick sehr einfach aussieht, ist jedoch wesentlich komplizierter. Es wirken verschiedene Einflussfaktoren, die der Bauphysik, Bauchemie, Konstruktion, dem jeweiligen Standort und dem Klima zu zuordnen sind. Diese können sich zum Teil aufheben oder auch verstärken. Hinzu kommt, dass in der Praxis sehr unterschiedliche Sachverhalte vorliegen, sodass diese nicht differenziert zugeordnet werden können.
Wurde früher den latenden Wärmebrücken wenig Beachtung geschenkt, so haben diese mit den hohen Anforderungen an den Wärmeschutz an Bedeutung gewonnen und können berechnete Werte der Wärmedämmung illusorisch machen. Hier ist die niedrige Oberflächentemperatur an der Innenseite von Bedeutung, da diese in vielen Fällen zu Feuchteschäden führen und so eine Grundlage für eine Schimmelpilzbildung oder im ungünstigen Fall auch zu einem Hausschwammbefall bilden. [20, 21]
Wärme- und feuchtigkeitstechnische Berechnungen können wichtige Hinweise auf eventuell Verbesserungen der Baukonstruktion geben. Es sind aber nur Näherungsrechnungen, die trotz hoch entwickelter Formeln keine übermäßige Präzision zulassen. Der Grund hierfür liegt darin, dass die Daten für die Berechnung zum Teil geschätzt werden müssen. Rohdichten müssen nicht immer zuverlässig sein, es sei denn, sie können einem Produktdatenblatt entnommen werden. Der Wert für die Wärmeleitung λ ist abhängig von der Rohdichte und dem Feuchtigkeitsgehalt. Trotz gleicher Ausbildung haben alle 4 Außenwände einen anderen Feuchtegehalt. Die TGL 35424/02 Tabelle 2 sah hier für die Berechnung des Wärmeleitwertes einen Korrekturfaktor vor, der die Feuchte berücksichtigen sollte. [22] Oswald schlug vor, dass die Temperatur in der Innenecke überschläglich mit einem verdreifachten inneren Wärmeübergangswiderstand berechnet werden kann. [23] In heutiger Zeit kommen zur Beurteilung der Auswirkungen der Temperaturerniedrigung sowie des Wärmeflusses Rechenprogramme zur Anwendung. [24, 25] Die zweidimensionale Berechnung erfolgt auf Basis der Methode der Finiten Elemente auf der europäische Grundlage EN ISO 10211.
Zunächst unterscheidet man die stofflichen und die geometrischen Wärmebrücken.
Die stoffliche Wärmebrücke entsteht an einer Außenwand durch die unterschiedlichen Wärmestromdichten bei mindestens zwei verschiedenen Baustoffen, die eine unterschiedliche Wärmeleitfähigkeit besitzen oder bei einem Baustoff mit gleicher Wärmeleitfähigkeit aber unterschiedlichen Querschnitten. Im ersten Fall könnten es Stahlbetonstützen einer beheizten Halle sein, die mit Leichtziegel ausgemauert wurden. Im zweiten Fall ein Leitungsschacht in der Außenwand.
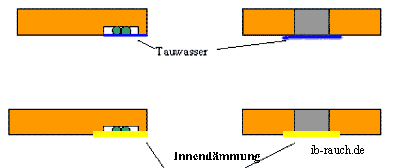
Diese Wärmebrücken lassen sich verhältnismäßig einfach beseitigen, in dem außen oder innen eine Wärmedämmung angebracht wird, sodass auf der gesamten Wandfläche ein gleichmäßiger Wärmefluss erreicht wird.
Bei der geometrischen Wärmebrücke sind die Stoffeigenschaften gleich, jedoch ist die innere und äußere Wandoberfläche unterschiedlich groß. In Mitteleuropa werden Gebäude gewöhnlich in viereckiger Form errichtet. Damit sind mindestens 4 geometrische Wärmebrücken vorhanden, wenn die Anschlüsse zum Dach und zur Bodenplatte nicht in die Betrachtung einbezogen werden.
Grundlage der thermodynamischen Betrachtung ist der 1. Hauptsatz, der wie folgt lautet:
Die Änderung der inneren Energie ist gleich der Summe der dem System in Form von Arbeit und Wärme zugeführte oder abgeführte Energie
q12+ wl2= u2- u1
mit w12= - 21∫pdv [1]
Die Gleichung wird auf ruhende geschlossene thermodynamische Systeme angewendet, z. B. im wärmeisolierten Gefäß als adiabatischer Prozess. Ein Gebäude kann nicht als wärmeisoliertes Gefäß betrachtet werden, auch wenn 5 oder 40 cm Wärmedämmung an die Außenwand angebracht werden. Es bleibt immer ein offenes thermodynamisches System. Die gegenwärtige energetische Betrachtung erfolgt auf der Grundlage stationärer Energieströme (DIN 4108 T.5). Darauf beruht die Berechnung des Wärmedurchgangskoeffizienten.
Es lässt sich Arbeit in Wärme und umgekehrt Wärme in Arbeit umwandeln, wobei stets die Größe der einen der anderen proportional ist. [2] Energie kann also weder aus Nichts entstehen noch in Nichts vergehen, sondern sich die einzelnen Energiearten nur ineinander verwandeln. Die Wärme kann nicht von selbst aus einem kälteren in einen wärmeren Körper übergehen. [3] Der Wärmestrom ist bei einem Temperaturunterschied vom wärmeren System in Richtung des weniger warmen Systems gerichtet, bis beide Systeme das gleiche Energieniveau erreichen.
Die Wärmebilanz bei einem Gebäude resultiert aus Teilströmen, wobei hier sich auf 4 Teilströme beschränkt werden soll.
a) Wärmeleitung, Wärmeaustausch zwischen Stoffoberfläche und dem (Bau)Stoff
b) Konvektion, Wärmeaustausch zwischen Gasgemisch (Luft) und Stoffoberfläche
c) Infrarotstrahlung, Wärmeaufnahme des (Bau)Stoffs durch Sonnenstrahlung oder IR-Heizung
d) Langwellige Strahlung, Wärmeaustausch zwischen Oberfläche und Umgebung [10]
Der Wärmedurchlasskoeffizient kennzeichnet die Wärmemenge, die in einer Stunde durch jeden Quadratmeter eines Bauteils bekannter Dicke im Dauerzustand der Beheizung hindurchgeht, wenn der Temperaturunterschied zwischen der Luft auf beiden Seiten dieser Wand 1 K beträgt. Nach Fourier ist der im Stoff geleitete Wärmestrom Q dem Temperaturgefälle dt/dx und der Wandfläche A senkrecht zum Wärmestrom proportional. Der Proportionalitätsfaktor λ (Wärmeleitfähigkeit) ist eine spezielle Eigenschaft der Stoffe, die im geringen Maß von Temperatur und Druck abhängig ist und experimentell ermittelt werden muss. Bei porösen Werk- und Baustoffen besteht eine Abhängigkeit zum Feuchtegehalt. In die Berechnung wird dies nicht berücksichtigt, obwohl sich die Größen erheblich verändern können.
Zum Beispiel:
Sand feucht: λ = 1,1 W/mK,
Sand trocken: λ = 0,33 W/mK oder
Eiche radial: λ= 0,17...0,31 W/mK, Eiche axial: λ= 0,37 W/mK. [4]
Wasser ist die beste Wärme leitende Flüssigkeit. Es besteht eine Temperaturabhängigkeit, bei 0ºC λ= 0,55 W/mK und 20ºC λ= 0,6 W/mK. [5]
Der Wärmedurchlasskoeffizient berechnet sich aus
Λ = λ/d [W/m2K]
Λ = Wärmdurchlasskoeffizient [W/m2K]
λ = Wärmeleitfähigkeit [W/mK]
d = Wandstärke [m]
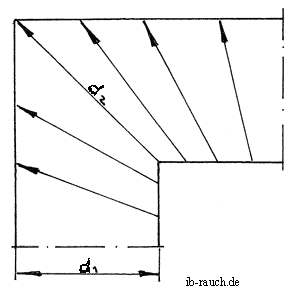
Bei diesem Beispiel handelt es sich um ein Mauerwerk aus Ziegel (1800) mit λ = 0,81 W/mK und einer Wandstärke 40 cm (1,5 cm Innenputz, Ziegel 36,5 cm und 2 cm Außenputz.) Die Pfeile in den Grafiken stellen vereinfacht die Richtung des Wärmeflusses dar. In Praxis sind diese jedoch verwirbelt.
Wärmdurchlasskoeffizient für die Außenwand:
Λ = λ/d1
= 0,81 W/mK / 0,40 m
= 2,0 W/m2K
Direkt in der Ecke ergibt sich für den Wandquerschnitt d2
d2 = √ d12 + d12 = √ 402 + 402
d2 = 56,6 cm
Damit ändert sich auch der Wärmedurchlasskoeffizient für die Außenecke.
Λ = λ/d2
= 0,81 W/mK / 0,566 m
= 1,54 W/m2K.
Bei dieser Konstruktion verringert sich aufgrund des größeren Wandquerschnitts der Wärmedurchlasskoeffizient um ca. 25%. Werden andere massive Baustoffe verwendet, zum Beispiel Leichtziegel (700) mit λ= 0,30 W/mK, so ergibt sich ein Verhältnis von 1,26 zu 0,53 [W/m2K] und bei Gasbeton (500) mit λ= 0,17 W/mK 0,42 zu 0,30 [Wm2K].
Zwischen beiden Systemen, innen und außen, kommt es ständig zum Energieausgleich, das heißt, es fließt zum Beispiel im Winter Wärmeenergie von innen nach außen. Der Wärmestrom nimmt den kürzesten Weg. Da aber im Eckbereich ein größeres Volumen des Mauerwerkes durchströmt werden muss, sind die Strömungsrichtungen in der angrenzenden Wandfläche in Richtung Ecke gerichtet. (Der Wärmestrom ist keine Gerade, wie in den skizzierten Bildern vereinfacht dargestellt, sondern eine Verwirblung.) Werden die Oberflächentemperaturen gemessen, so sind das in der Ecke Streifen von ca. 10-15 cm. Je weiter die Wärmeflüsse von der Ecke entfernt sind, so sind diese dann im rechten Winkel nach außen gerichtet. Nach diesem Sachverhalt müsste an der konstruktiven Ecke an der Innenseite eine höhere Oberflächentemperatur vorliegen, als an der übrigen Wandfläche. Dem ist es aber nicht so.
Durch die Eckenausbildung sind die gegenüberliegenden Wandoberflächen unterschiedlich groß. Die innere Oberfläche, die die Wärme aufnimmt, muss eine größere Außenfläche mit Wärme "versorgen".
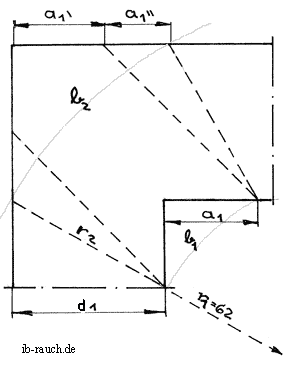Mit welcher Größenzunahme zu rechnen ist, kann nicht genau bestimmt werden. Für eine genaue Berechnung ist die Wärmezuführung durch Konvektion oder Wärmestrahlung zu bestimmen. Entscheidend ist aber auch, ob die Zimmerecke verstellt oder frei zugänglich ist. Hierzu währe eine sehr aufwende Berechnung erforderlich. Für eine stark vereinfachte Betrachtung werden zwei Kreisbögen konstruiert. Der Wärmeaustausch erfolgt gradlinig durch den Wandquerschnitt. Problematisch ist hier nur den Mittelpunkt des Kreises festzulegen. Befindet sich zum Beispiel eine Strahlenheizung gegenüber im Raum, so könnte der Radius r1 4 oder 5 m betragen. Damit ist der Winkel α klein und für den Bogen b2 ergibt sich damit nur eine kleine Vergrößerung. Befindet sich dagegen ein unisoliertes Heizrohr direkt in der Zimmerecke, so ist der Winkel α sehr groß. Damit wird der Bogen b2 ebenfalls groß. In Betrachtung der zahlreichen Möglichkeiten fällt es schwer, die Innenfläche a1 zu bestimmen. Der Bogen berechnet sich aus
b= r x arcα .
Je nachdem, wie groß der Radius r1 gewählt wird, ergibt sich ein Verhältnis von r1 zu r2 mit circa 1 zu 1,5. Die Summe aus dem Wandquerschnitt 1 und der betrachteten Wandfläche a1 dürfte die maximal erreichbare Außenfläche ( a1'+a1'') entsprechen. Für die Wandfläche außen a2 gilt:
(d1 + a1) > a2 > b2
a1 b1
Die Wandfläche im Eckbereich ist außen damit mindestens 50% größer als die innen liegende. An der Außenwandoberfläche geht die Wärme auf die umgebende Luft über. Dies wird durch den Wärmeübergangskoeffizienten αa berücksichtigt. Geht man davon aus, dass dieser Übergang an allen Stellen gleichgroß ist, so muss an der Innenseite an allen Wandabschnitten die gleiche Wärmemenge zugeführt werden. An der Innenseite der Zimmerecke ist aber diese Fläche kleiner. Es kann in einer bestimmten Zeiteinheit nicht so viel Wärme aufgenommen werden. Es kommt damit zu einer Absenkung der Oberflächentemperatur, was der um ca. 25% kleinere Wärmedurchlasskoeffizient im Eckbereich nicht kompensieren kann. In der nachfolgenden Berechnung werden Messwerte aus einer Untersuchung herangezogen. (Siehe hier die Tabelle unter ib-rauch.de/Beratung/schimmel-beispiel.html.)
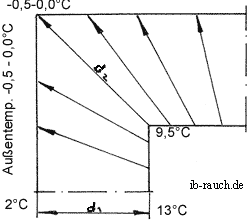In einer Erdgeschosswohnung mit dem oben genannten Wandaufbau wurde die Oberflächentemperaturen innen und außen
gemessen. Die Lufttemperatur außen betrug -0,5 bis 1,0ºC, die Oberflächentemperatur 2ºC und die Temperatur an der Ecke 0,0 bis 0,5ºC. Die gegenüberliegende Temperatur in der Ecke betrug 9,5ºC und an der Innenwand 13ºC. (Diese niedrigen Werte lagen in Fußbodenhöhe vor, die Zimmertemperatur betrug 19ºC, Erfassung am 16.3.2006, 8.00 Uhr.)
In der nachfolgenden Berechnung wird der theoretische Wärmestrom an der Außenwand und in der Ecke bezogen auf ein Quadratmeter bestimmt.
Für die Wandfläche:
A (ϑ1 - ϑ2) 1 m2 (13ºC - 2ºC) 11 Wm2K
Q1 = -------------- = ------------------------- = --------------- = 22,3 W
s1/λ 0,4 m / 0,81 W/mK 0,49 m2K
Für die Ecke:
A (ϑ1 - ϑ2) 1 m2 (9,5ºC - 0ºC) 9,5 Wm2K
Q2 = -------------- = ---------------------------- = --------------- = 13,6 W
S1/λ 0,566 m / 0,81 W/mK 0,7 m2K
In der nachfolgenden Berechnung wird der Wärmestrom an einer Außenwand mit einer viereckigen Grundfläche von 16 m2 und einer o. g. massiven Wand mit 40 cm und einer Temperaturdifferenz von 20 K sowie ein Vieleck (Zylinder) mit gleicher Wandstärke verglichen. Für die Flächenberechnung wird eine Höhe von 1 m angenommen.
|
Wärmestrom an einer ebenen Fläche U = a1 + a2 + a3 + a4 = 4,8 + 4,0 + 4,8 + 4,0 [m] = 17,6 m
Berechnung Wärmestrom A (ϑ1 - ϑ2) 17,6 m2 x 20 K Q = -------------- = ------------------------ d1/λ 0,4 m / 0,81 W/mK 352 m2K = ----------------- = 712,8 W 0,494 m2K/W
|
Wärmestrom in einem Vieleck (Kreis) r1 = √ A/Π = √ 16m2/ 3,14 = 2,26 m r2 = r1 + s = 2,26 m + 0,4 m = 2,66 m 2 Π 1 m (ϑ1 - ϑ2) Q = ---------------------- 1/ λ x ln r2/r1
2 x 3,14 x 1m x 20 K = --------------------------------------- 1/0,81 W/mK x ln 2,66m/2,26m
125, 6 W = ------------------ = 624,9 W 0,201 |
Auch aus Sicht der Betrachtung eines Vielecks wird deutlich, dass geometrische Ecken nicht zwangsläufig zu einem höheren Wärmestrom führen. Was aber von Bedeutung ist, ist die unterschiedliche Wärmeübertragungsfläche einmal an der Innen- und Außenseite.
Es sind weitere praktische Untersuchungen erforderlich, um die verschiedenen Einflussfaktoren genauer bestimmen zu können und auch mögliche Fehler auszuschließen. In diesem Zusammenhang soll auch darauf verweisen werden, dass bisher geometrische Wärmebrücken im instationären Bereich nicht gemessen wurden. Diese sind zur Untermauerung des Aussagewertes der theoretischen Betrachtungen erforderlich.
Aus gegenwärtiger Sicht unterliegen die Ausgangswerte für die bauphysikalische Berechnung zur Bewertung der Wärmeverluste an den Wandecken gemäß der DIN [26] einer gewissen Ungenauigkeit. So dient der angenommene Wert der Wärmeleitfähigkeit des Wandbaustoffs als Rechengröße für die Bestimmung der Wärmstromdicht. Die dieser fließt dann als Rechengröße in den thermischen Leitwert
L2D = q / ( θi – θ e)
und somit auch in den ψ-Wert (lineare Wärmedurchgangskoeffizient bzw. Wärmebrücken-Verlustkoeffizient) ein.
ψ = L2D – U x l
Der Wärmedurchgangskoeffizient „ …ergibt sich aus der Differenz des thermischen Leitwerts L2D aus der Wärmebrückenberechnung und dem Produkt aus U- (Λ)-Wert und Länge l des ‚ungestörten’ Bauteils, in diesem Fall der jeweils ebenen Wandkonstruktion…“ [27]
In den folgenden Bildern wurden Infrarotaufnahmen an einer Außenwandecke von innen aufgenommen. Sie zeigen deutlich den Temperaturunterschied im Eckbereich. Bei Gösel [14] erfolgt eine prozentuale Verteilung der Wärmeströme durch eine monolithische, außen und innen gedämmte Außen- und Innenecke mit u= 0,6 W/m²K, θ i = 20°C und θ a = -10°C. Für
In einer theoretischen Betrachtung sind Rimal/Hermes [27] zu einer ähnlichen Feststellung gekommen, dass eine massive Wandkonstruktion mit äußerer Wärmedämmung zu einem größeren Wärmeverlust führt, als eine ohne Wärmedämmung. (Die ebenen Wandflächen haben jeweils einen U-Wert = 0,3 W/m2K.)
Für eine nachträgliche Temperierung unterkühlter massiver Innenwandecken bietet sich somit eine Innendämmung an. Hier besteht jedoch das Problem, dass die kühlere Wandoberfläche an eine andere Stelle verlagert wird.
© Altbausanierung | Bauideen | Blog | Sanierungskosten | Wohnen | Impressum | AGB/Datenschutzerklärung | 7/2018 
